概率论参考文章

把研究一群研究对象称作总体,每个研究对象称为个体。
例如:我们研究一群学生的身高。看似总体是一群学生,个体是每个学生。实际上总体是一群数字,个体是每一个数字。在这个总体中,有的数字出现的多,有的出现的少,因此用一个概率分布去描述这个总体是很合适的,从这个角度,总体就是概率分布。
为了了解总体的分布,我们从总体中随即抽取n个个体,称之为总体的一个样本。n为样本容量,样本中的个体称之为样品
- 样本具有随机性:即总体中每个个体被抽到的概率相等
- 样本要有独立性:即每个样本的的取值,不影响其他样本的抽取
抽取样本的观测值没有具体的数值,只有一个范围
例如:总体是一群学生的身高,(160-170)有10人,(170-180)有20人,(180-~)有10人。
设是样本个体,假设是有序样本,定义如下函数:
对样本数据
-
对样本进行分组:确定组数k,平均每组样品3,4个
-
确定每组组距:$$d = dfrac{(max-min)}{组数}$$
-
确定每组组限:$$a_0,a_0+d=a_1,a_0+2d=a_2,cdots$$ 形成一下区间$$(a_0,a_1],(a_1,a_2],cdots,(a_{k-1},a_k]$$ 。
-
统计样本数据落入每个区间的个数(频数),并列出其频数频率分布表
-----分组区间---- -----组中值---- 频数 频率 ... ...
略。
样本来自总体,因此样本中含有总体各个方面的信息,但这些信息较为分散,为将这些分散的信息集中起来反应总体的各种特征,需要对样本加工,最常用的方法是构造样本的函数,不同的函数反应总体的不同特征。
样本均值用表示:
在分组样本的场合:
其中为组数,为第组的组中值,为第组的频数
-
方差
-
标准差:
-
无偏方差:
在这个定义中: 称之为偏差平方和,称之为偏差平方和的自由度。
- 总体分布为,则的精确分布为。
- 若总体不是正态分布, 渐进分布为。
- 阶原点矩:$$a_k=dfrac1 n sum x_i^k$$ ,一阶原点矩就是均值
- 阶中心距:$$b_k=dfrac1 n sum(x_i-bar x)^k$$,二阶中心距就是方差。
当总体关于分布中心对称时,用刻画总体的特征就很有代表性。
当不中心对称时,我们需要引入样本偏度和样本峰度来刻画总体。
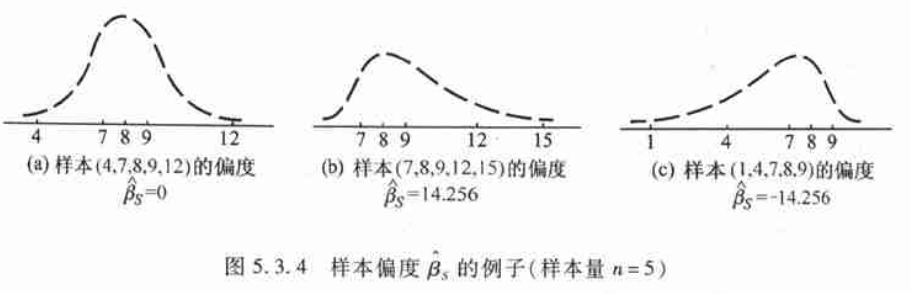
样本偏度(中心距的函数)
反映总体分布与对称性的偏离方向及程度
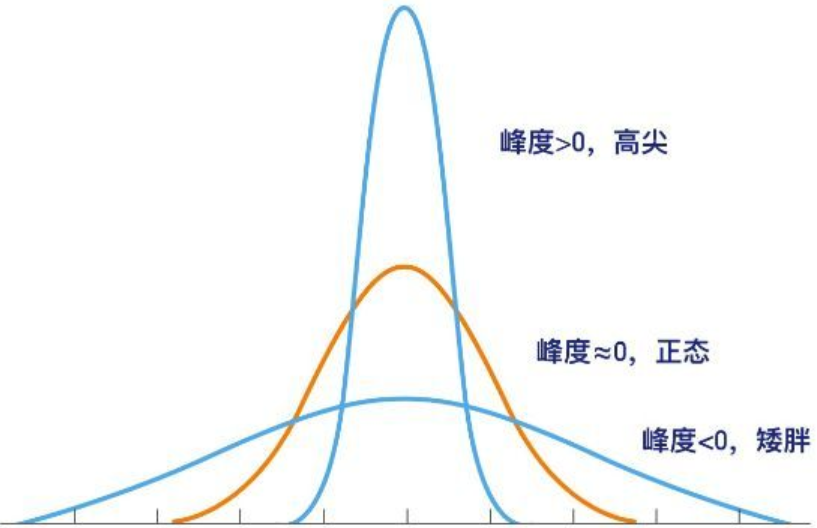
样本峰度
反映总体分布曲线在其峰值附近的陡峭程度和尾部粗细的统计量。
当明显大于0,陡峭,尾部细。
对样本从小到大排序,第个就是样本的第次序统计量,记作。
单个次序统计量的分布
设总体的密度函数,分布函数,则第次序统计量的密度函数为
多个次序统计量的联合分布
.
样本矩代替总体距,用代替.
有几个未知参数,就列几个方程 .
总体分布列为为未知参数. 为样本观测值,
. 为似然函数,选取,使的值尽量大。
离散情况下,是分布列,连续情况下是密度函数。
- 先写出似然函数
- 对似然函数取对数,求导,求最大值。
.
.
对给定的, ,称随机区间为的置信水平为的置信区间。
事先给定,再求置信区间。
- 构造,分布已知,不依赖于任何未知参数
- 选择两个常数,使得.。。。。
- 将变形为置信区间
选取枢轴量, 置信区间为
选取枢轴量, 置信区间为
选取枢轴量, 置信区间为 .
-
已知时的两样本区间
选取枢轴量 ,置信区间为
-
未知时的两样本区间
尽量不要拒绝原假设,也就是尽量小。
为拒绝域 ,为拒绝的概率,犯错误的概率


